Interpolating data

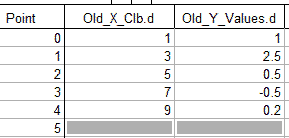
Why interpolate?

When working with experimental data, most of the time we use a X-Y pair data model. In this model values of independent and dependent variables are given by two waves with equal number of points. Pairs of values found in both waves at the same position (or point #) determine coordinates of the value on a 2D graph. The table below shows an example:

Old_X_Clb represent X coordinate (example: amount of reactant added) Old_Y_Values represent Y coordinate (example: measured signal)	This pair can be plotted as a graph:

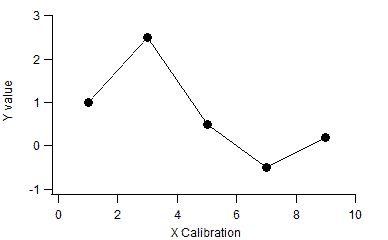
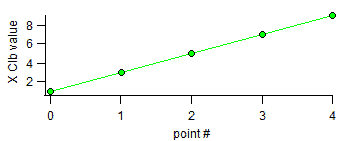
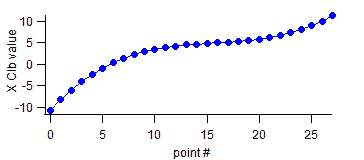
If you need to know response at one of experimental points (5 or 7, for example), you can look up exact values from the table or graph (using Ctrl-I tool). However, you do not have exact response at other, intermediate calibration points (3.5 or 6.12, for example). Another example of such problem arises when you compare spectra measured with different resolutions or using different instruments. Each instrument has its accurate wavelength calibration, but such calibrations will not match between instruments. While you can compare spectra on the same graph using two separate X-Y pairs, you cannot add or subtract such spectra because wavelength calibrations of corresponding points in spectra do not match. In order to allow such spectral calculations you need to perform interpolation of one the spectra.

Interpolation

Interpolation allows to calculate what the new XY pairs would be based on existing data.

Assume that we have an old XY pair (Old_Y_Values vs Old_X_Clb from above) measured with low-resolution spectrometer. In this case X calibration is linear (i.e. changes from point to point by the same amount):

Now assume that you need to use these data for calculation on data from a high-resolution spectrometer. On only those data have more points and smaller calibration step from point to point, but wavelength calibration is also non-linear (step varies from point to point), as is the case in most real systems. Let's call this wave New_X_Clb:

To calculate what the values of Old_Y_Values would be if measured on the high-resolution system with New_X_Clb calibration instead of low-resolution Old_X_Clb we can calculate a new wave New_Y_Values using Interpolate2 command:

interpolate2 /L=3 /T=1 /X=New_X_Clb /Y=New_Y_Values Old_X_Clb, Old_Y_Values

Where:

• /L=3 tells Igor to use interpolation at values specified by /X= flag
• /T=1 specifies linear interpolation as the way to calculate new values
• /X=New_X_Clb gives the wave gives calibration values at which new Y values should be calculated (should exist)
• /Y=New_Y_Values gives the name of the wave where new values should be stored (does not need to exist)
• Old_X_Clb, Old_Y_Values specifies the old X-Y pair to use in calculating new values

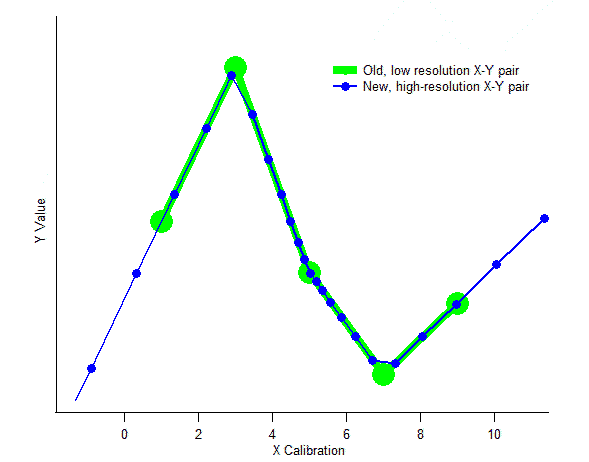
This graph illustrates such interpolation for the old X-Y pair and new calibration used in the example above:

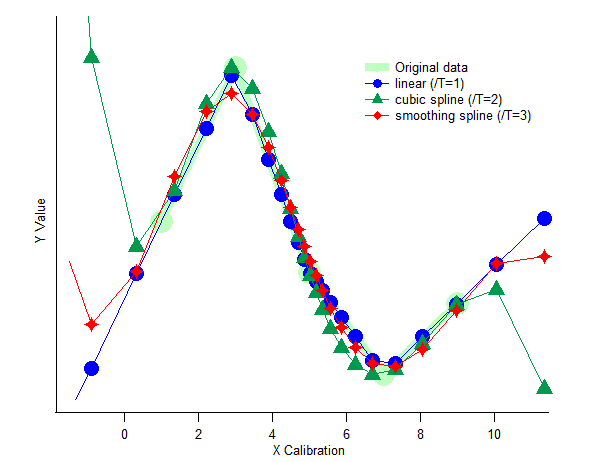
Igor provides several methods of interpolating data (controlled by the /T= flag) illustrated here: